02. ControlArray
Sunhyup Lee. (2024). To be a successful candidate for the coding test. goldenrabbit. p.112.
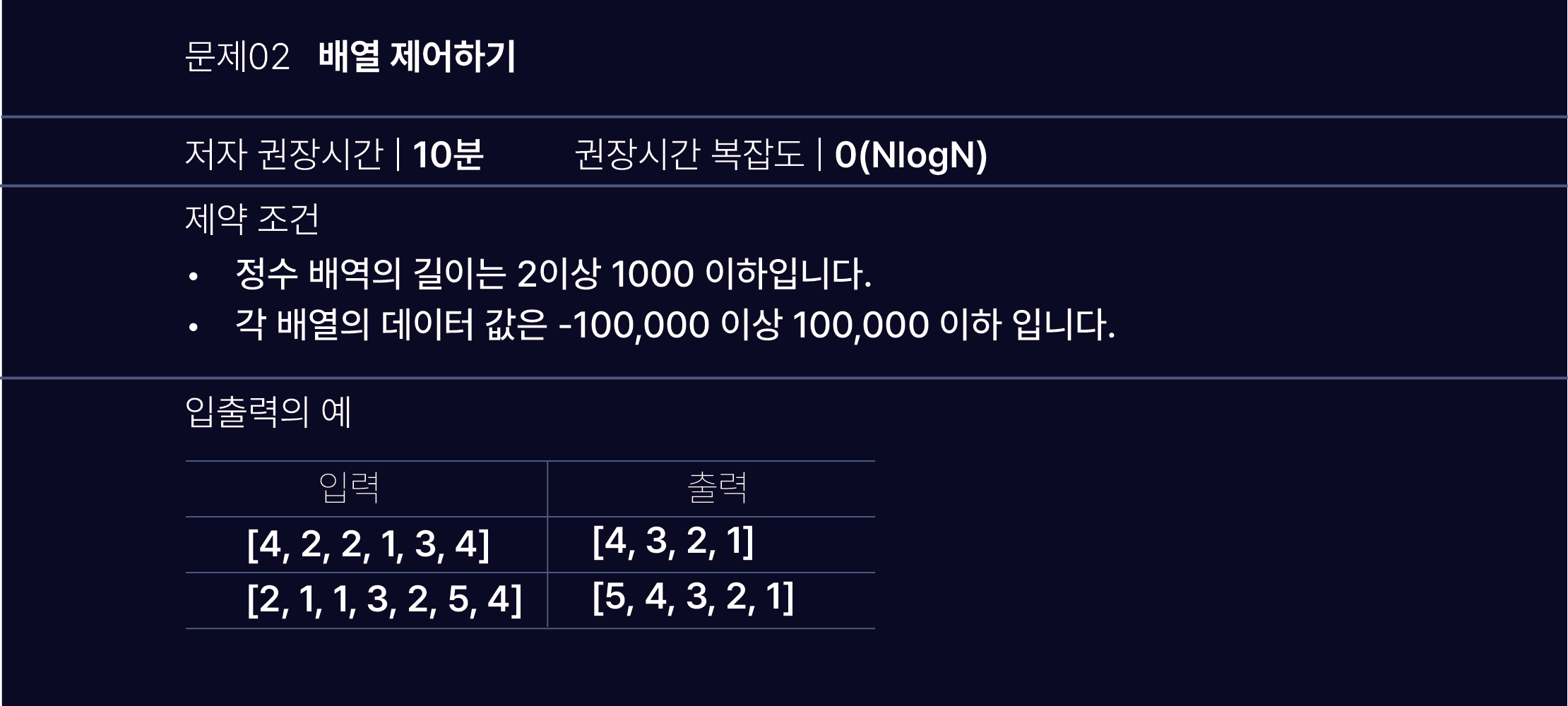
Problem solving
다양한 방식으로 배열을 제어해보자
① The first way to solve the problem : 내장된 빌트엔 메서드(set)를 사용해보자!
function solution(arr) {
const uniqueArr = [...new Set(arr)];
uniqueArr.sort((a, b) => b - a);
return uniqueArr;
}
🧐 시간복잡도는 어떨까?
1) new Set(arr) 중복제거: O(n)
2) […new Set(arr)] 배열변환 O(n)
3) uniqueArr.sort((a, b) => b - a) 정렬: O(n log n) (일반적으로 소요)
최종 시간 복잡도: O(n) + O(n) + O(n log n) = O(n log n)
② The second way to solve the problem : filter + indexOf를 이용해보자!
function solution(arr) {
const uniqueArr = arr.filter((value, index) => arr.indexOf(value) === index);
uniqueArr.sort((a, b) => b - a);
return uniqueArr;
}
🧐 시간복잡도는 어떨까?
1) filter 와 indexOf 메서드 결합하여 호출: O(n2)
2) sort 메서드는 일반적으로 O(n log n) 소요
최종 시간 복잡도: O(n) + O(n) + O(n log n) = O(n2)
③ The third way to solve the problem : map을 사용하여 중복제거
function solution(arr) {
const uniqueObj = {};
arr.forEach(value => {
uniqueObj[value] = true; // value를 uniqueObj 객체의 키로 설정하고, 그값을 true로 지정
});
const uniqueArr = Object.keys(uniqueObj).map(Number); // key를 배열로 만들고 숫자로 타입변환
uniqueArr.sort((a, b) => b - a);
return uniqueArr;
}
🧐 시간복잡도는 어떨까?
1) forEach 메서드: 최종 시간 복잡도:O(n)</span>
2) Object.keys 메서드: 최종 시간 복잡도:O(n)</span>
3) sort 메서드: 최종 시간 복잡도:O(n log n)</span>
최종 시간 복잡도: O(n) + O(n) + O(n log n) = O(n log n)
④ The fourth way to solve the problem : reduce를 사용하여 중복제거
function solution(arr) {
const uniqueArr = arr.reduce((acc, value) => {
if (!acc.includes(value)) {
acc.push(value);
}
return acc;
}, []);
uniqueArr.sort((a, b) => b - a);
return uniqueArr;
}
🧐 시간복잡도는 어떨까?
1) reduce 메서드는 배열의 각 요소에 대해 include 메서드를 호출 : O(n2)
2) sort 메서드: O(n log n)
최종 시간 복잡도: O(n) + O(n) + O(n log n) = O(n2)
⑤ The fifth way to solve the problem : 정렬 후 중복제거
function solution(arr) {
arr.sort((a, b) => b - a);
const uniqueArr = [];
for (let i = 0; i < arr.length; i++) {
if (i === 0 || arr[i] !== arr[i - 1]) {
// 배열의 첫 번째 요소(arr[0])는 항상 고유한 값으로 간주되며, 비교할 이전 요소가 없기 때문에 무조건 uniqueArr에 추가 + arr[i]가 이전 요소 arr[i - 1]와 다른지를 확인합니다.
uniqueArr.push(arr[i]);
}
}
return uniqueArr;
}
🧐 시간복잡도는 어떨까?
1) sort 메서드: O(n log n)
2) 중복 제거 루프: O(n)
최종 시간 복잡도: O(n) + O(n log n) = O(n log n)
⑥ The sixth way to solve the problem : 두 포인터 사용
function solution(arr) {
arr.sort((a, b) => b - a);
const uniqueArr = [];
let i = 0;
while (i < arr.length) {
uniqueArr.push(arr[i]);
let j = i + 1;
while (j < arr.length && arr[j] === arr[i]) {
j++;
}
i = j;
}
return uniqueArr;
}
/*
1) i와 j의 상호작용을 통해 중복된 값들을 효율적으로 건너뛰면서 배열을 탐색합니다. i는 고유한 값을 가리키고, j는 중복된 값을 건너뛰어 다음 고유한 값의 위치로 i를 이동시킵니다.
2) 이 과정에서 i는 중복된 값들을 건너뛰고 j가 가리키는 새로운 위치로 점프합니다. 이렇게 함으로써, 배열을 한 번만 순회하면서 중복을 제거할 수 있습니다.
*/
🧐 시간복잡도는 어떨까?
1) sort 메서드: O(n log n)
2) 두 포인터 루프: O(n)
최종 시간 복잡도: O(n log n) + O(n) = O(n log n)