05. Multiplication of matrices
Sunhyup Lee. (2024). To be a successful candidate for the coding test. goldenrabbit. p.122.
Problem solving
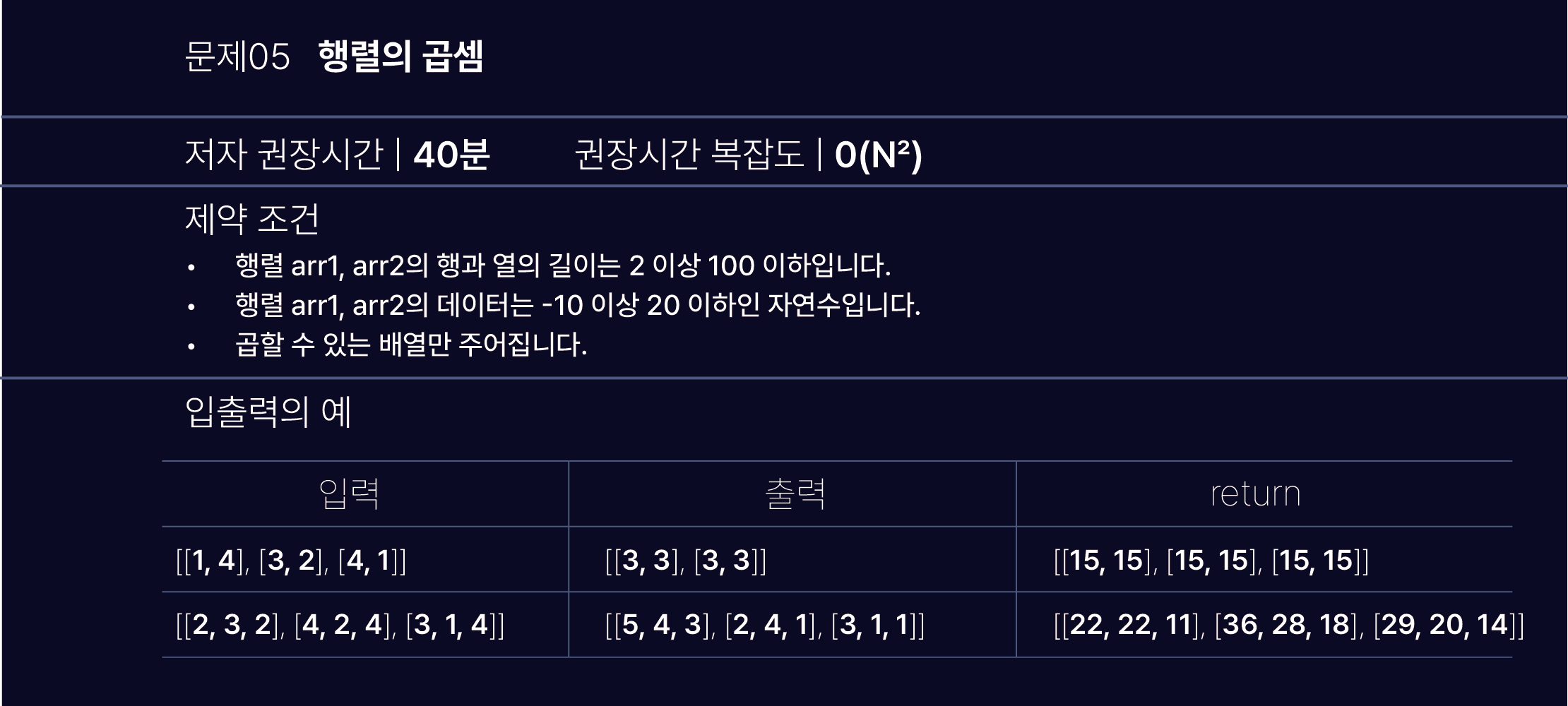
2차원 행렬 arr1과 arr2를 입력받아 arr1에 arr2를 곱한 결과를 반환하는 solution( ) 함수를 완성
① The first way to solve the problem : for문 이용해서 풀기
function solution(arr1, arr2) {
const r1 = arr1.length;
const c1 = arr1[0].length;
const c2 = arr2[0].length;
const ret = [];
for (let i = 0; i < r1; i++) {
ret.push(new Array(c2).fill(0));
}
// ⬇ 이러한 방식은 어떨까? 좀 더 명확하게 각 변수의 역할을 강조
const ret = Array.from({ length: r1 }, () => Array(c2).fill(0));
for (let i = 0; i < r1; i++) {
for (let j = 0; j < c2; j++) {
for (let k = 0; k < c1; k++) {
ret[i][j] += arr1[i][k] * arr2[k][j];
}
}
}
return ret;
}
🧐 시간복잡도는 어떨까?
[Done] exited with code=0 in 0.063 seconds
최종 시간 복잡도: O(n3)
② The second way to solve the problem : map과 reduce를 사용한 풀이
function solution(arr1, arr2) {
const r1 = arr1.length;
const c1 = arr1[0].length;
const c2 = arr2[0].length;
return arr1.map((row, i) =>
arr2[0].map((_, j) =>
row.reduce((sum, _, k) => sum + arr1[i][k] * arr2[k][j], 0)
)
);
}
좀더 직관적으로 표현해보자면,
function solution(arr1, arr2) {
return arr1.map((row, i) =>
arr2[0].map((_, j) =>
arr1[i].reduce((sum, val, k) => sum + val * arr2[k][j], 0)
)
);
}
<특징>
이 방법도 함수형 스타일로 작성되어 있지만,
배열 전개 방식(즉, 각 배열의 요소를 명확하게 펼쳐서 처리)을 더 명시적으로 사용한다.
여기서 arr1[i].reduce()를 사용하여 첫 번째 행렬의 𝑖번째 행의 값을 더 직접적으로 순회합니다.
<차이>
첫 번째 방식에서는 row.reduce()에서 arr1[i][k]를 다시 참조했지만,
이 방식에서는 명시적으로 val을 곱셈에 사용합니다.
🧐 시간복잡도는 어떨까?
[Done] exited with code=0 in 0.068 seconds
1) r1의 시간 복잡도: arr1의 행의 개수
2) c1의 시간 복잡도: arr1의 열의 개수 소요
3) c2의 시간 복잡도: arr2의 열의 개수 소요
최종 시간 복잡도: O(r1 x c1 x c2)