20. a runner who did not finish the race

Problem solving

1. 하나하나 대조하며 완주하지 못한 사람 찾기

알고리즘의 시간 복잡도는 O(N^{2)인데 마라톤 경기에 참여한선수는 최대 10만 명으로 가정했기 때문에 이보다 더 나은 O(NlogN) 또는 O(N)알고리즘을 찾아야 한다.}

2. 하나하나 대조하며 완주하지 못한 사람 찾기

완주자의 이름을 참여자에서 바로 찾을 수 있다면 알고리즘의 시간 복잡도를 많이 낮출 수 있을 것 같다. 배열 인덱스와 같은 방식으로 특정 데이터에 바로 접근할 수는 없을까? 이를테면 마라톤 참가자 이름 자체를 인덱스처럼 쓰면 좋을 것 같다.

키는 마라톤 참가자 이름으로 값은 키를 가진 마라토너의 수로 표시하면,

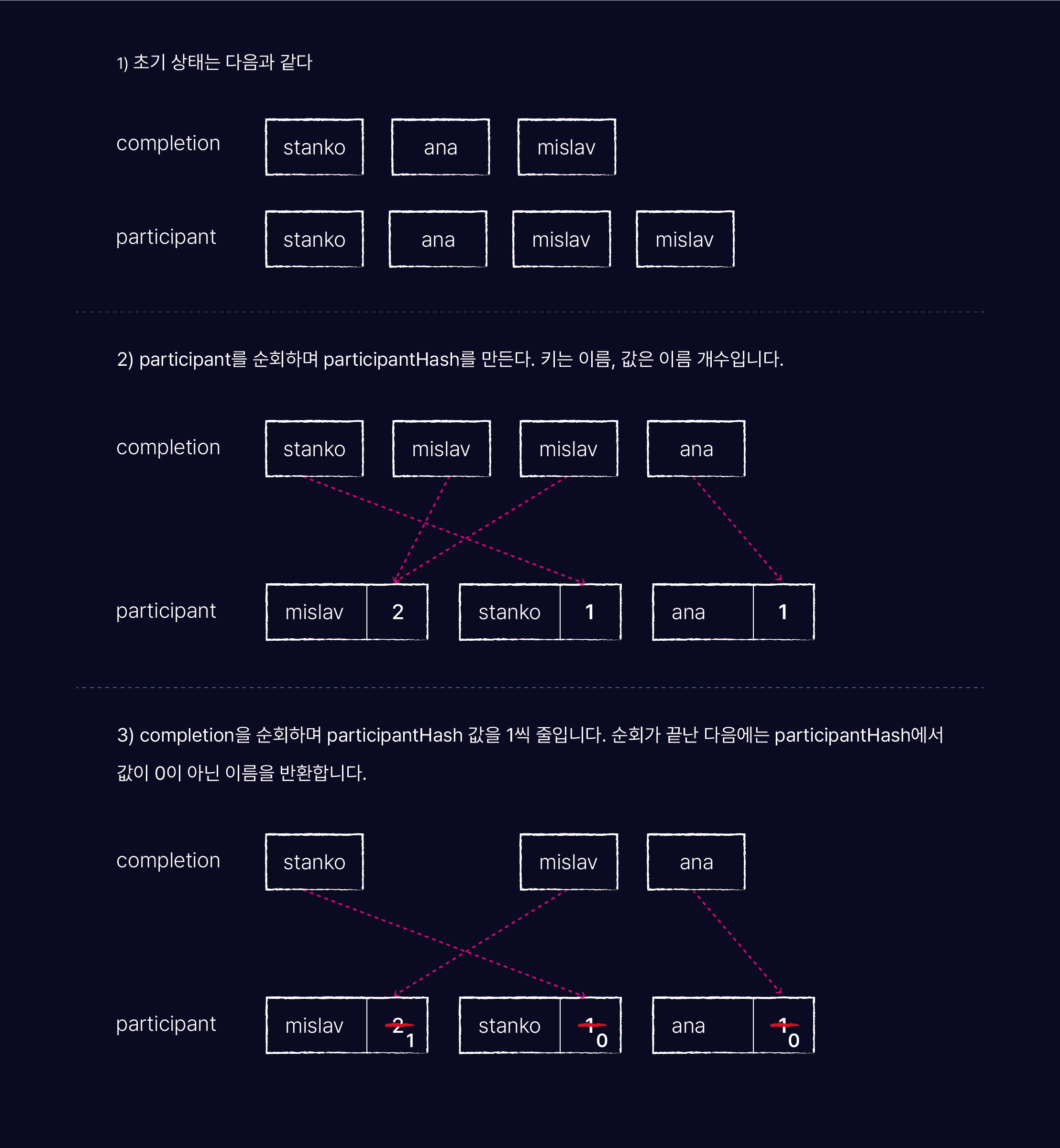
2.1 참가자들의 이름을 해시 테이블에 추가하되, 키-값은 (이름-이름개수)로 한다.

2.2 완주한 선수들의 이름을 해시테이블에서 찾아 값을 1씩 줄인다.

2.3 해시를 순회해서 값이 0이 아닌 키(이름)를 반환한다.

function solution(participant, completion) {
  const obj = {}; // ① 해시 테이블 생성

  for (const p of participant) {
    // ② 참가자들의 이름을 해시 테이블에 추가
    if (obj[p]) {
      obj[p] += 1;
    } else {
      obj[p] = 1;
    }
  }
  for (const c of completion) {
    // ③ 완주한 선수들의 이름을 키로 하는 값을 1씩 감소
    obj[c] -= 1;
  }
  for (const key in obj) {
    // ④ 해시 테이블에 남아 있는 선수가 완주하지 못한 선수
    if (obj[key] > 0) {
      return key;
    }
  }
}

🧐 Q. 왜 전체 순회는 O(N), 카운팅은 O(1)인가?

Answer)

1. 참가자들의 이름을 순회하며 테이블을 만드는 작업: O(N)

for (const p of participant) {
  if (obj[p]) {
    obj[p] += 1;
  } else {
    obj[p] = 1;
  }
}

이 작업의 시간 복잡도:

1. participant 배열의 순회:

   • 크기가 N인 배열을 한번 순회하므로 O(N)

2. 해시 테이블 데이터 추가 또는 갱신:

   • 각 참가자 이름(p)에 대해;

     • 해시 함수로 테이블에서 키를 찾아 값을 삽입하거나 갱신합니다.
     • 이 과정은 평균적으로 O(1)입니다.

   • 따라서, N번 삽입 작업을 반복해서 시간 복잡도는: O(N) x O(1) = O(N)

2. 완주 여부에 따라 값을 감소하는 작업: O(M)

for (const c of completion) {
  obj[c] -= 1;
}

이 작업의 시간 복잡도:

1. completion 배열을 순회:

   • 크기가 M인 배열을 한 번 순회하므로 O(M)

2. 해시 테이블에서 감소:

   • 각 완주자 이름(c)에 대해:

     • 해시 함수로 키를 찾아 값을 감소합니다.
     • 이 작업의 평균적으로 O(1)입니다.

   • 따라서, M번의 감소 작업을 반복해도 시간복잡도는: O(M) x O(1) = O(M)

3. 해시 테이블 생성이 O(N), 값 감소가 O(1)인 이유

해시 테이블 생성 O(N):

• 전체 참가자 배열(participant)를 순회하며 각 이름을 해시 테이블에 추가하거나 갱신합니다.
• N개의 데이터를 처리해야 하므로 전체적으로 O(N)

값 감소 작업 O(1):

• 개별적으로 O(1): 해시 함수는 키를 계산하고, 테이블에서 해당 위치에 직접 접근하여 값을 변경합니다.
• 따라서, 특정 키에 대해 값을 갑소하는 단일 작업의 시간 복잡도는 평균적으로 O(1)입니다.

4. 결론

• 참가자들의 이름을 순회하여 테이블을 만드는 작업: O(N)
• 완주 여부에 따라 값을 감소하는 작업: O(M)
• 따라서, 코드 전체의 시간 복잡도는: O(N) + O(M) = O(N+M)